Цитата дня

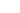
Ориентация жизни в существенных вопросах на интеллект, как правило, идет рука об руку с проникновением денежного хозяйства; в сфере торговли интеллект обладает полнотой суверенитета. Усиление интеллектуальных, абстрагирующих способностей характеризует эпоху, в которой деньги все больше превращаются в чистый символ и становятся индифферентными к своей собственной ценности.
Цитата из книги: «Философия денег»
Новинки книги нон-фикшн













Смотреть все
Новинки аудиокниг













Смотреть все
Бестселлеры нон-фикшн 













Смотреть все
Анонсы нон-фикшн








Смотреть все
Книги издательства Владос
Книги издательства Алетейя
Детская и юношеская книга
Книги издательства Страта
Книги ДМК Пресс
Нон-фикшн недели

Сегодня Рейчел Карсон назвали бы экологом, но дело в том, что именно благодаря ей экология и возникла. Ведь каких-то 70 лет назад ученые все еще видели в природе врага, которого необходимо покорить, будь то с помощью пестицидов или энергии атома. Мысль о том, что от сохранности хрупкой экосистемы Земли зависит судьба человечества, никому и в голову не приходила. Рейчел Карсон была первой, кто открыл людям эту очевидную истину с помощью своих удивительных книг, в которых научные факты вплетены в трогательную, поэтическую прозу.
Книга «Океан вокруг нас», опубликованная в 1951 году и переведенная на 29 языков, является одной из самых успешных познавательных книг о природе для широкой читательской аудитории в истории мировой литературы. В 1952 году она получила Национальную книжную премию и медаль Джона Берроуза, а в 1953 году по ней был снят одноименный документальный фильм (The Sea Around Us), удостоенный премии «Оскар».
Топ книг Директ-Медиа